"Si realmente has entendido algo, es que puedes
explicáraselo a tu abuela" (Albert Einstein). Y
de esta manera yo la he comprendido y pretendo explicarla.
Físicos precursores
Ya para mediados del siglo XIX se pensaba que la luz, como onda electromagnética y
similar a la del agua, sonido, etc. debería poseer un medio de propagación; se lo llamó
"Éter".
Entre otros teóricos y experimentadores, cobró notoriedad el llamado "experimento
de Michelson y Morley" realizado en 1887 que pretendía medir las
características de este medio de propagación, pero el resultado fue fallido porque
hallaron que no existía.
Seguido y para ampliar estos resultados los físicos FitzGerald en 1889 y Lorentz en 1892
obtuvieron lo que se denominó la "contracción
de Lorentz".
Luego es Einstein en 1905 que postula la Teoría de la Relatividad Especial (o
Restringida) y la amplía para 1915 incluyendo la afectación de la masa de los
cuerpos, esto es, la gravedad (sistemas inerciales), y la llama Teoría de la
Relatividad General.
Premisas
Para comprender los desarrollos relativistas y sus conclusiones, se deberán
acepetar dos principios:
- La velocidad de la luz en el vacío (aproximadamente el
aire) es siempre constante; esto es, que es independiente del marco de referencia u
observador. La llamaremos "c" y vale más o menos 300.000.000 [km/s]. Es éste un concepto irracional. Y, además, como si fuera poco
esto, se debe saber que no puede estar en reposo (un fotón no puede detenerse en vacío,
aunque sí en un medio cristalino como se ha logrado por un minuto hace unos años por
ejemplo en la Universidad Técnica de Darmstadt, Alemania).
- Que la energía y la masa no son necesariamente lo mismo,
sino "manifestaciones" de lo mismo. Esto se puede
demostrar analíticamente y comprender si pensamos que dándole calor a un objeto podemos
obtener más calor de él. Para poder llevar esto a una ecuación de igualdad se ha visto
que la constante de proporcionalidad es "c2": E[J] = m[g].c2
La contracción de Lorentz
§ La contracción longitudinal
Realizaremos un "experimento del pensamiento". Pensaremos que
nos encontramos dentro del vagón de un tren en movimiento y posamos en el suelo una
linterna encendida que alumbre al techo, y un segundo observador se halla fuera. Y
llamaremos con el nombre "propio" a todo lo que nos sucede a nosotros e
"impropio" a lo del sujeto fuera.
Tendremos por tanto tres variables a considerar en el recorrido de la luz que siempre lo
hará a una velocidad "c" donde la velocidad "v" del vagón no
influirá en la trayectoria lumínica
donde tp = tiempo propio (nuestro dentro del vagón); ti = tiempo
impropio (o sea del observador afuera del vagón); x, h = espacios impropios; y = espacio
propio.
Si planteamos por Pitágoras la hipotenusa "h" podremos deducir con los
planteos precedentes el factor de Lorentz "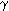 " "
y con ello la contracción del espacio y la dilatación del tiempo
y = h / 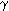  contracción de la
trayectoria "y" contracción de la
trayectoria "y"
tp = y / c = (h / 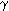 )
/ c = [(c.ti) / )
/ c = [(c.ti) / 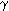 ]
/ c = ti / ]
/ c = ti / 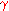  dilatación del tiempo propio "tp"
(o sea que ti > tp) por Lorentz dilatación del tiempo propio "tp"
(o sea que ti > tp) por Lorentz
Así, cuando "y" se inclina (o sea que "h" aumenta) se
apreciará en el camino la contracción del espacio por Lorentz
xp = x / 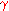  contracción del
espacio propio "xp" (o sea que x = xi > xp) por Lorentz contracción del
espacio propio "xp" (o sea que x = xi > xp) por Lorentz
Y es de esperar que si el espacio disminuye, también lo haga su tiempo, porque de
otra manera la ousía (esencia del objeto u "objeto sustancial")
se modificaría. En otros términos, al avanzar el vagón para el observador externo el
espacio-tiempo del viajero se contrae: por ejemplo un metro-segundo en éste implicará
más metros-segundos en el observador fijo. Conceptualmente y de manera sencilla: si el espacio aumenta 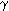 veces, también obviamente lo hará en veces, también obviamente lo hará en 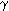 el tiempo, y viceversa. Por
tanto, un viaje al futuro sin regreso perfectamente se da en cada ousía que
aumenta su velocidad con respecto a la otra. el tiempo, y viceversa. Por
tanto, un viaje al futuro sin regreso perfectamente se da en cada ousía que
aumenta su velocidad con respecto a la otra.
En una anotación matricial abreviada podríamos escribir esto como [sp;
tp] = [si; ti] / 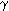 donde s> es el vector indicador de las 3
dimensiones y cuyo módulo por Pitágoras resulta s = donde s> es el vector indicador de las 3
dimensiones y cuyo módulo por Pitágoras resulta s = 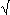 [x2 + y2
+ z2]. [x2 + y2
+ z2].
Por otro lado, aclaramos para hacer extensivo este ejemplo a nuestras vidas y
experiencias, de más estará decir que no todos andamos por allí presentando una
linterna y apuntándola al techo, ni los objetos con que nos relacionamos disponen de
ella, sino que "siempre la llevamos con nosotros en el bolsillo ( )" y, de no ser así,
"urgente" aprópiese de una para que estos efectos también valgan con usted. )" y, de no ser así,
"urgente" aprópiese de una para que estos efectos también valgan con usted.
§ La contracción tangencial
De manera análoga a la anterior, realizaremos un "experimento del
pensamiento". Pensaremos que nos encontramos ahora dentro de un vehículo
espacial rotando alrededor de un centro imaginario.
La masa relativista
Cuando un objeto que posee una masa en reposo "m" viaja a una velocidad
"v" como en el ejemplo precedente, por ejemplo dentro del mismo vagón o por
cuenta propia, la misma cambia para el observador afuera. Esto lo podemos deducir
partiendo de la aceleración propia que psee "ap"
ap = 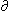 v
/ v
/ 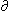 tp = tp = 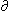 (x/ti) / (x/ti) / 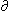 tp = tp = 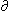 (x/ti) / (x/ti) / 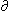 (ti / (ti / 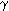 ) = ) = 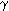 . . 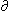 (vi)
/ (vi)
/ 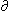 (ti i
= (ti i
= 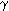 . ai . ai
donde por la fuerza "f" por Newton y el principio de conservación de la
energía podemos igualar
fi = m. ap = mi. ai
resultando finalmente una masa relativista "mi" que
aumenta con la velocidad de la misma manera y proporcional que el factor de Lorentz
m 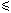 mi = m mi = m 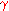 <
< 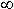  ampliación
de la masa ampliación
de la masa
y por ello la ecuación original de la Relatividad Especial (Restringida)
debe corregirse de una manera General así
E = m 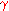 c2 c2  energía y masa equivalente mi energía y masa equivalente mi
La masa curva el espacio-tiempo
Ofrecida por Einstein como la "Idea más feliz de su vida",
presentó la correspondencia entre la gravedad terrestre como un caso similar al de lo que
ocurre en un sistema inercial ordinario, denominando al efecto como "Principio de
la Equivalencia".
En otras palabras, lo que vimos con anterioridad en "§ La contracción
tangencial" se da también para un objeto de masa "m" posado sobre una
esfera. En otros términos, para este objeto el espacio-tiempo se verá afectado 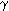 veces. veces.
O sea, se concluye, que la masa curva al espacio-tiempo también en su derredor.
Cuanto más nos acercamos de su centro, más se "contraerán" tanto el espacio
como el tiempo para un observador fuera del sistema, y el objeto o individuo que vive este
acercamiento al centro ni se entera.
Es bastante común que se represente este
efecto tridimensional con mallas, embudos o colchones que son deformados por una bola
pesada, y luego haciendo girar una bolilla para representar el efecto de que
"cae" al centro. Nada más desacertada, desafortunada y ridícula
ejemplificación, quiero aclarar esto. Si se usara un colchón nuevo ( ), que no se hunda y se aprecie el
efecto en un plano, entonces no habría ejemplificación que valga. No hay
"caída", se debe desmitificar esto. ), que no se hunda y se aprecie el
efecto en un plano, entonces no habría ejemplificación que valga. No hay
"caída", se debe desmitificar esto.
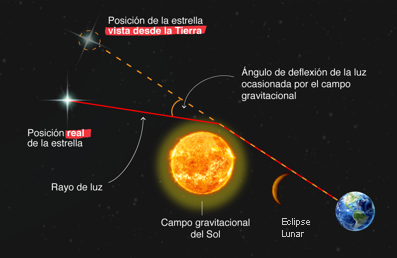
La experiencia de Eddington
Para el año 1919 el físico Eddington corrobora estos principios relativistas al
medir la trayectoria curva de la luz de una estrella que se encontrara por detrás del Sol
en una observación de eclipse lunar para aprovechar la situación y poder fotografiarla.
|
|
La iluminación que identifica a
una estrella, es decir su rayo de luz que nos llega, pensado como fotones en marcha,
debido a la gran masa del Sol su espacio en derredor se contrae y "desvía" la
trayectoria del haz. Seguido y por la inercia que poseen estos fotones con su masa
equivalente continúan su viaje y se reciben en la Tierra.
|
|
|
|
La Gravedad relativista
Es éste un concepto de difícil aprensión. Para abordar el tema se es consciente
que deben acuñarse los conceptos de la matemática de los espacios curvos de Riemann, los
tensores, etc. Pero he encontrado una manera sencilla igual de comprenderlo, y a eso
apunto.
Nos valdremos de lo que se ha explicado en el apartado precedente de "§ La
contracción tangencial" y de la experiencia de Eddington.
|
|
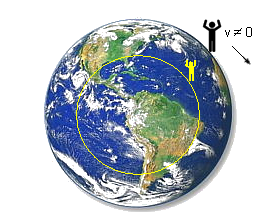
Así, un objeto o nosotros mismos
detenidos sobre la superficie terrestre, equivaldremos a un sistema inercial viajando
tangencialmente sobre la superficie de la Tierra a la velocidad de su propia rotación.
Por tanto, nuestro verdadero camino para no falsear la relación entre el perímetro y su
diámetro, que es  ,
necesariamente convergeremos a un diámetro menor que se encuentra dentro del propio
planeta. Es así como no podremos desprendernos de su superficie porque la misma nos frena
llegar a este régimen de estabilidad. ,
necesariamente convergeremos a un diámetro menor que se encuentra dentro del propio
planeta. Es así como no podremos desprendernos de su superficie porque la misma nos frena
llegar a este régimen de estabilidad.
Por eso es importante la experiencia de Eddington, porque supera el "Principio de
Equivalencia"; es decir, que muestra la independencia de la contracción
espacio-temporal de un concepto de rbita inercial.
Dicho de otra manera, la curvatura del espacio-tiempo que producimos al rotar nos
implicará un recorrido que no puede ser otro que el interno al planeta, y por eso
"caemos", la gravedad de la masa de la Tierra nos "ha atraído" (por
decirlo de alguna manera) según la gnoseología newtoniana. |
|
| |
La Gravedad Newtoniana y la Einstiana
La que hemos visto hasta ahora, la relativista, es la que también se podría llamar
Einstiana (o bien Aristotelista). La otra, es la de Newton. Ésta última puede
ejemplificarse para campos de fuerza gravitatorios einstianos débiles.
La primera en la historia del ser humano ha sido la de Aristóteles al observar con su
sencillez e ingenuidad que "cada cuerpo tiende a ir a ocupar su lugar natural",
donde la locación que le ha dado la Naturaleza para el equilibrio. Esta idea formaba
parte de su filosofía natural y cosmología, y ha sido un precursor conceptual de las
teorías modernas de la gravedad (entre otros temas).
La segunda, ya científica y extraordinaria, fue planteada por Newton, donde observara que
la gravedad es una fuerza de atracción entre masas, o podríamos decir de partículas
atómicas según su peso. Su famosa ecuación será por todos conocida:
f = m1. m2. G / d2
donde f [N] es la fuerza de atracción entre los cuerpos, m1 [kg] y m2
[kg] sus masas respectivas, G [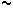 6,674. 10-11
[m3/kg.s2] una constante gravitatoria universal de proporcionalidad
y d [m] la distancia entre los centros de las masas. 6,674. 10-11
[m3/kg.s2] una constante gravitatoria universal de proporcionalidad
y d [m] la distancia entre los centros de las masas.
De tal manera esto es cierto, que cuando un objeto está posado sobre el suelo, nos cuesta
despegarlo (levantarlo).
Ahora, en tercera aparición, viene la Teoría de la Relatividad de Einstein, que como se
indicó en este apartado y tal cual
se volviera a lo anticipado por Aristóteles, los objetos tienden a un lugar estable
dentro del planeta. Y que no es necesariamente un "fuerza".
Entonces, allí viene la pregunta: "¿Es al final la gravedad una fuerza o no lo
es?". Bien, la respuesta en primera instancia sería, al igual que la dualidad
onda-partícula de la luz, que posee ambas interpretaciones y que se ajustarían a tal o
cual fenómeno para explicarlo.
Pero debemos saber que (al menos para mi compensión), no es así. Hay una sola verdad y
es la segunda: la einstiana, donde para campos de gravedad débiles se la puede aproximar
a la newtoniana. Veamos seguidamente esto.
Así, hay algunas formas de ver cómo la gravedad newtoniana emerge
como una aproximación de la relatividad general. Una forma de ver la aproximación
es considerar el límite de campo débil en la relatividad general. En este límite, la
métrica del espacio-tiempo se puede escribir como una perturbación pequeña de la métrica
de Minkowski:
gµ = hµ
= hµ + hµ + hµ
donde hµ es la métrica
de Minkowski y hµ es la métrica
de Minkowski y hµ es una perturbación pequeña. es una perturbación pequeña.
En este límite, las ecuaciones de Einstein se pueden linealizar y se obtienen ecuaciones
que describen la propagación de ondas gravitacionales y la interacción entre la materia
y el campo gravitatorio.
En el límite de velocidades pequeñas y campos débiles, las ecuaciones de Einstein
linealizadas se reducen a la ecuación de Poisson para el potencial gravitatorio:
 2 F = 4 2 F = 4 Gr Gr
donde F es el potencial gravitatorio,
G es la constante de gravitación universal y r es la densidad de masa.
Y, a partir de esta ecuación, se puede derivar la fuerza gravitatoria que actúa sobre
una partícula de prueba:
f = - m  F F
que es la fuerza gravitatoria newtoniana.
En este sentido, las ecuaciones de aproximación que relacionan la relatividad general con
la gravedad newtoniana son:
- Las ecuaciones de Einstein linealizadas, que describen la propagación de ondas
gravitacionales y la interacción entre la materia y el campo gravitatorio en el límite
de campo débil.
- La ecuación de Poisson para el potencial gravitatorio, que se obtiene en el límite
newtoniano.
Estas ecuaciones muestran cómo la gravedad newtoniana emerge como una aproximación de la
relatividad general en el límite de velocidades pequeñas y campos débiles
|
| |
Resumen
Primero, partimos del hecho de que la velocidad de la luz siempre es constante, sin
importar quién esté observando o dónde y cómo se encuentre.
En el ejemplo del vagón de un tren (contracción de
Lorentz donde simplemente se muestra que cuando un pasajero ve dentro de él un
recorrido de un haz de luz, el que está fuera lo ve también pero con un derrotero
mayor), se muestra que cuanto más rápido nos movemos, más corto es nuestro tiempo. Esto
significa que, a medida que nuestra velocidad aumenta, el tiempo pasa más rápido para
nosotros en comparación con alguien que está en reposo.
Dado que nuestro cuerpo no cambia de forma al movernos, podemos deducir que el espacio que
recorremos también se comprime en la dirección en la que nos desplazamos. Y en la misma
proporción que el tiempo.
Aparentemente estamos quietos en la superficie de la Tierra, pero en realidad nos movemos
con ella debido a su rotación. Esto implica que nuestro recorrido sobre ella no es el del
perímetro completo del planeta, sino uno menor.
Este camino más corto explica por qué permanecemos adheridos al suelo, puesto que
nuestro perímetro de derrotero es menor. |
|
|
|